連載コラム『数理最適化』
第2回 数理最適化とは②
2016.10.24
第1回に引き続き、「数理最適化とはどういったものなのか?」というテーマでご紹介したいと思います。
最適化の具体的なイメージを理解していただくため、簡単な問題を一緒に解いてみましょう。
最適化の具体的なイメージを理解していただくため、簡単な問題を一緒に解いてみましょう。
最適化問題:ナップザック問題
あなたは野菜を袋に入れて持って帰ろうとしています。
野菜は1種類につき1個ずつあり、組み合わせて袋に入れることが出来ます。
しかし、手元にある袋には重さの制限があり、5kgまでしか入りません。
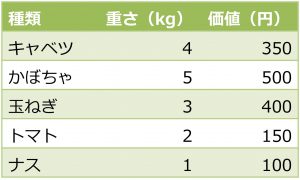
持ち帰る野菜の価値の合計を最も高くするにはどの野菜を選択すればいいのでしょうか?


野菜は1種類につき1個ずつあり、組み合わせて袋に入れることが出来ます。
しかし、手元にある袋には重さの制限があり、5kgまでしか入りません。
持ち帰る野菜の価値の合計を最も高くするにはどの野菜を選択すればいいのでしょうか?



表を見ると、もっとも価値の高い野菜はかぼちゃ(500円)です。
しかし、袋にはかぼちゃ1つしか入りません。
重さ5kgという制限の中で、500円の価値を超えるような複数の野菜の組み合わせはないでしょうか。
| キャベツ (4kg:350円) |
+ | ナス (1kg:100円) |
= | 5kg:450円 |
| 玉ねぎ (3kg:400円) |
+ | ナス (1kg:100円) |
= | 4kg:500円 |
| トマト (2kg:150円) |
+ | ナス (1kg:100円) |
= | 3kg:250円 |
| 玉ねぎ (3kg:400円) |
+ | トマト (2kg:150円) |
= | 5kg:550円 |

色々な組み合わせが考えられますが、玉ねぎとトマトを選ぶことで550円という最大の価値を得ることができました。これが最適解となります。
こういった問題は、一般的にナップザック問題と呼ばれ、代表的な最適化問題の1つです。
こういった問題は、一般的にナップザック問題と呼ばれ、代表的な最適化問題の1つです。
最適化は難解
例として挙げた問題は一目瞭然なほど簡単ですが、もし野菜の数を20種類とし、袋の容量を50kgまでとしたらどうなるでしょうか?
 野菜の組み合わせが膨大な数となり、先ほどのように一つひとつのパターンを検証していくやり方では、人間はもちろん、コンピュータが行っても気が遠くなるほどの時間がかかってしまいます。(野菜の組み合わせはなんと約100万(2^20)通り!)
野菜の組み合わせが膨大な数となり、先ほどのように一つひとつのパターンを検証していくやり方では、人間はもちろん、コンピュータが行っても気が遠くなるほどの時間がかかってしまいます。(野菜の組み合わせはなんと約100万(2^20)通り!)
実際にはさらに多くの組み合わせや制約条件の中で解を求める事になるので、非常に難解な問題だと言えます。
 野菜の組み合わせが膨大な数となり、先ほどのように一つひとつのパターンを検証していくやり方では、人間はもちろん、コンピュータが行っても気が遠くなるほどの時間がかかってしまいます。(野菜の組み合わせはなんと約100万(2^20)通り!)
野菜の組み合わせが膨大な数となり、先ほどのように一つひとつのパターンを検証していくやり方では、人間はもちろん、コンピュータが行っても気が遠くなるほどの時間がかかってしまいます。(野菜の組み合わせはなんと約100万(2^20)通り!)実際にはさらに多くの組み合わせや制約条件の中で解を求める事になるので、非常に難解な問題だと言えます。
この問題を解くには?
上記のような、最適化問題を解くための方法は2つあります。
①厳密な最適解を得る“厳密解法”
②現実的な時間でなるべく良い解を効率よく得る“近似解法”
②現実的な時間でなるべく良い解を効率よく得る“近似解法”
今回の連載テーマである数理最適化は厳密解法に分類されます。
まとめ
第1~2回でご紹介した内容をまとめます。
- 数理最適化とは数学的手法で最適な解を導出すること
- 数理最適ソルバとコンピュータの進歩により、大きな問題も解けるようになってきた
- 検証すべき組み合わせの数が膨大となるため、最適化問題は非常に難解な問題である
- 最適化問題を解く方法は、厳密解法と近似解法の2つに分類される
次回は、最適化問題を解くための方法である、厳密解法と近似解法の特徴と相違点について紹介したいと思います。
この連載のバックナンバーはこちら




