連載コラム
『数理最適化』
第3回 最適化手法
2016.11.14
第1~2回では、「数理最適化とはどのようなものなのか」をご紹介しました。
今回は、最適化における手法の種類と特徴についてご紹介したいと思います。
今回は、最適化における手法の種類と特徴についてご紹介したいと思います。
最適化問題を解くための2つの方法
第2回の最後にご説明しましたが、最適化問題には2つの解法があります。
①厳密な最適解を得る“厳密解法”
②現実的な時間でなるべく良い解を効率よく得る“近似解法”
②現実的な時間でなるべく良い解を効率よく得る“近似解法”
それぞれの解法は「どのような特徴を持っているのか」「どのようなアプローチがあるのか」について紹介していきます。
厳密解法について

厳密解法は最適化問題に対する最も良い解を求める手法です。
厳密解法で求められた解は、数学的に最適であると証明されているということになります。
しかし、最適解を求めるためには多くの計算時間が必要となるため、大きすぎる問題は扱えない場合があります。
厳密解法で求められた解は、数学的に最適であると証明されているということになります。
しかし、最適解を求めるためには多くの計算時間が必要となるため、大きすぎる問題は扱えない場合があります。
近似解法について

近似解法は、現実的な時間でなるべく良い解を効率よく得る手法です。
厳密解法と違い、求めた解は最適性を保証されませんが、高速に近似解を求めることができます。
厳密解法と違い、求めた解は最適性を保証されませんが、高速に近似解を求めることができます。
厳密解法と近似解法の使い分け

実際に最適化問題を解く場合、厳密解法と近似解法のどちらを適用すればよいのでしょうか?
多くの場合、まずは厳密解法を適用してみます。
問題の難しさや規模によって現実的な時間で解けない場合、近似解法を適用することになります。
これまでは近似解法でないと解けない問題がほとんどでした。
しかし、数理最適ソルバとコンピュータの進歩により、現実的な問題にも厳密解法が適用できるようになっており、近年注目されてきています。
多くの場合、まずは厳密解法を適用してみます。
問題の難しさや規模によって現実的な時間で解けない場合、近似解法を適用することになります。
これまでは近似解法でないと解けない問題がほとんどでした。
しかし、数理最適ソルバとコンピュータの進歩により、現実的な問題にも厳密解法が適用できるようになっており、近年注目されてきています。
各々の解法に関する手法を体系的にまとめると、以下のようになります。
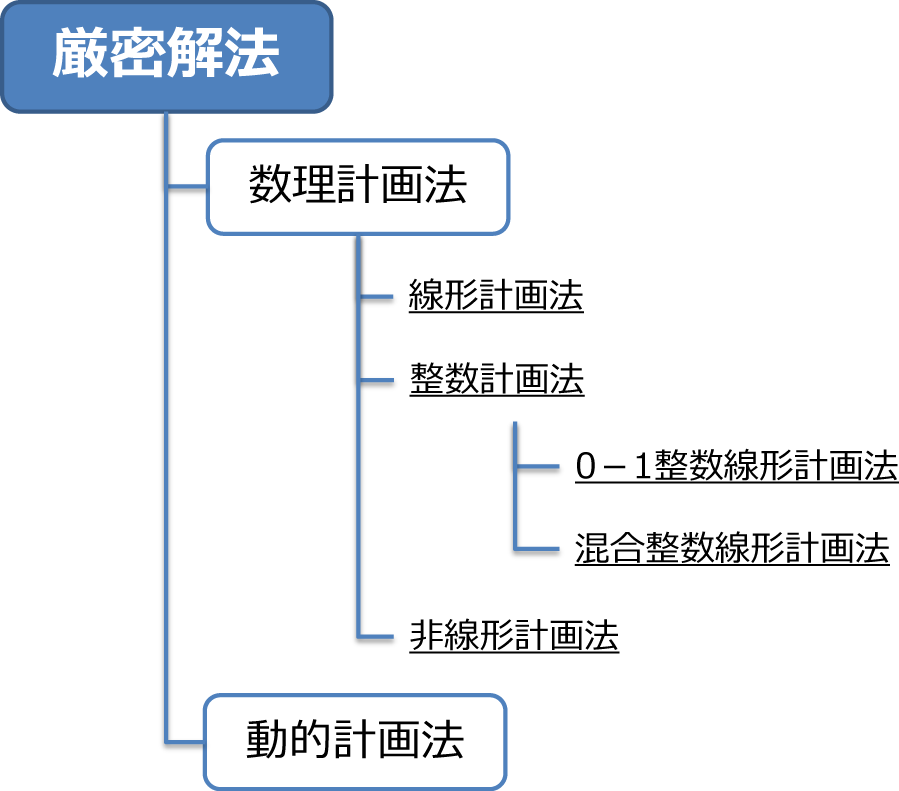
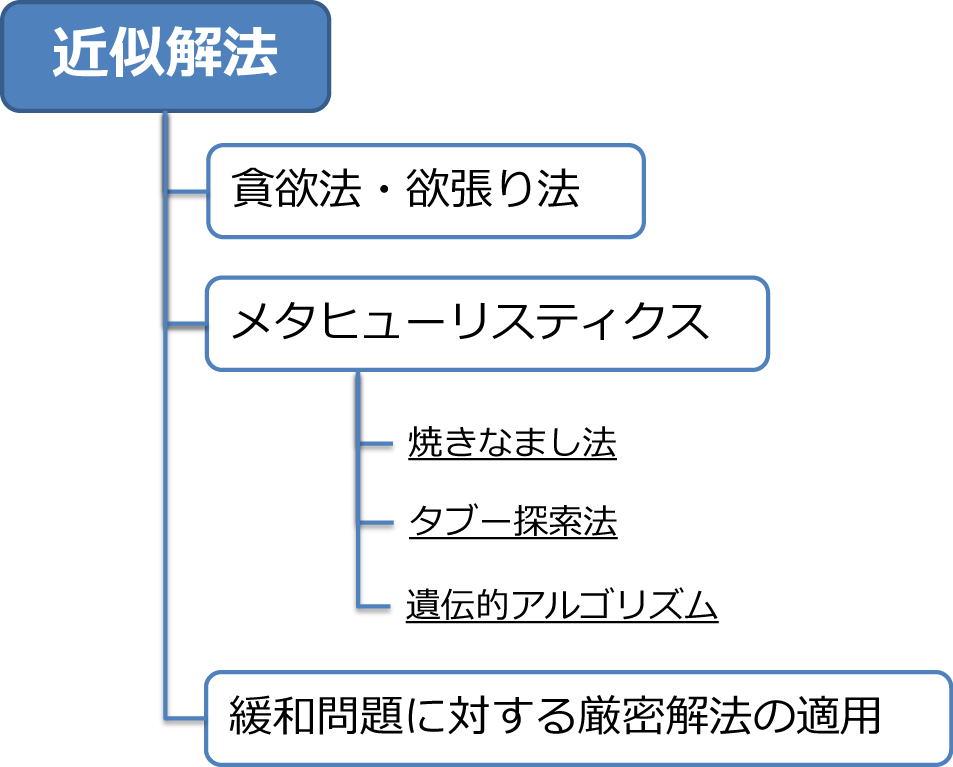
次回、この連載のテーマである数理最適化について、手法の特徴に踏み込んだ内容を紹介したいと思います。
この連載のバックナンバーはこちら




