連載コラム
『数理最適化』
第4回 数理最適化とその歴史①
2016.12.5
第3回では、「最適化の手法の種類と特徴」をご紹介しました。
今回より、「厳密解法である数理最適化はどのようにして解を出すのか?」という点に関して、数学者達の発案の歴史に焦点を当てながら「各手法の特徴」を紹介したいと思います。
今回より、「厳密解法である数理最適化はどのようにして解を出すのか?」という点に関して、数学者達の発案の歴史に焦点を当てながら「各手法の特徴」を紹介したいと思います。
最適化問題の種類と解法
最適化問題はいくつかの種類があり、それに対する解法が存在します。
はじめに線形計画法が発案され、それを応用して整数計画法と非線形計画法へと発展しました。
はじめに線形計画法が発案され、それを応用して整数計画法と非線形計画法へと発展しました。
| 線形計画問題 | ← | 線形計画法 (Linear Programming, LP) |
| 整数計画問題 | ← | 整数計画法 (Integer Programming, IP) |
| 非線形計画問題 | ← | 非線形計画法 (Nonlinear Programming, NLP) |
今回は“線形計画問題”について紹介します。
線形計画問題(Linear Programming Problem)
“線形計画問題”は一次式や一次不等式で表される制約条件の中で、一次式の目的関数を最大化または最小化する問題です。イメージしやすいように例題をご用意しました。
今回の目的はミネラル摂取量の最大化でした。
ユーカリAの質量をx、ユーカリBの質量をyとすると、
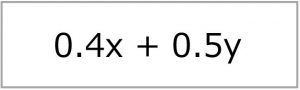
これを最大化することになります。
次に、今回の制約条件を一次不等式で表してみましょう。
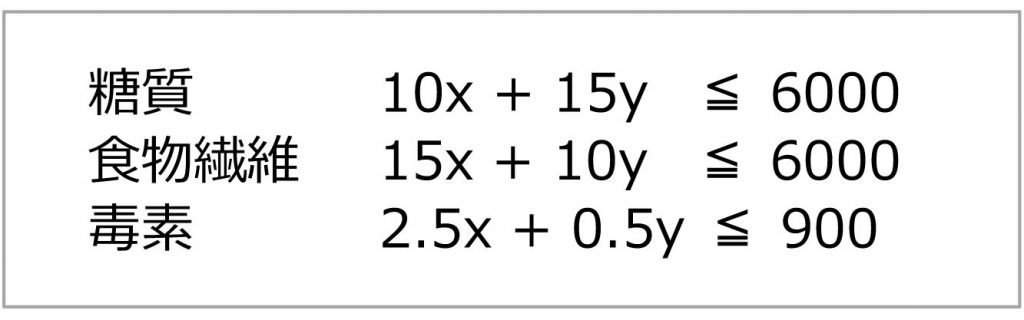
これらの条件式から目的関数を求め、グラフ化すると以下の図のようになります。
横線で塗りつぶされた領域が制約条件を満たす範囲(実行可能領域)となり、この中から最も良い解を探索することになります。
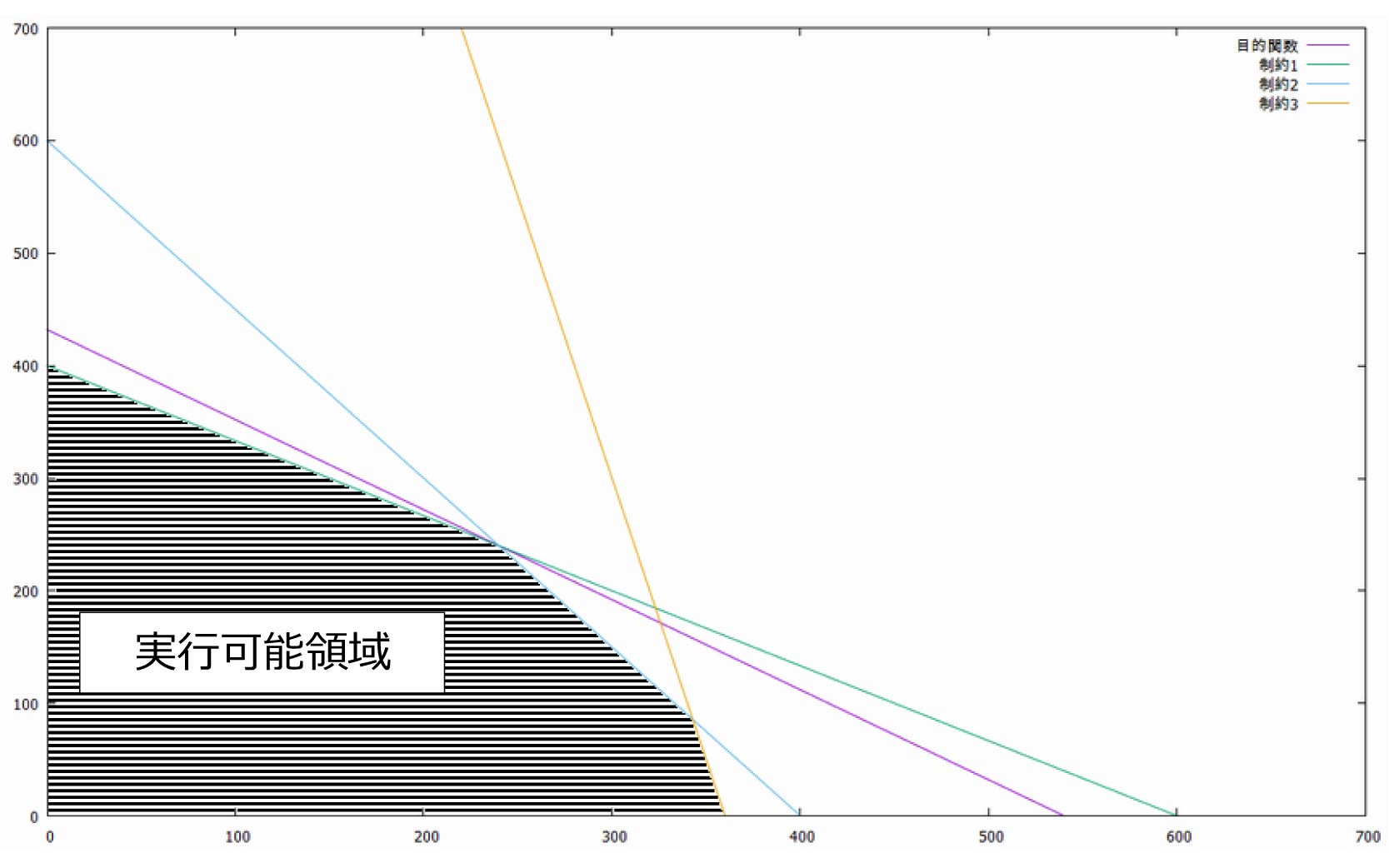
最適化問題の中では最も簡単な問題であり、高速に解を得られる解法が存在します。
その中でも代表的なものとして、以下の2つの方法があります。
例題
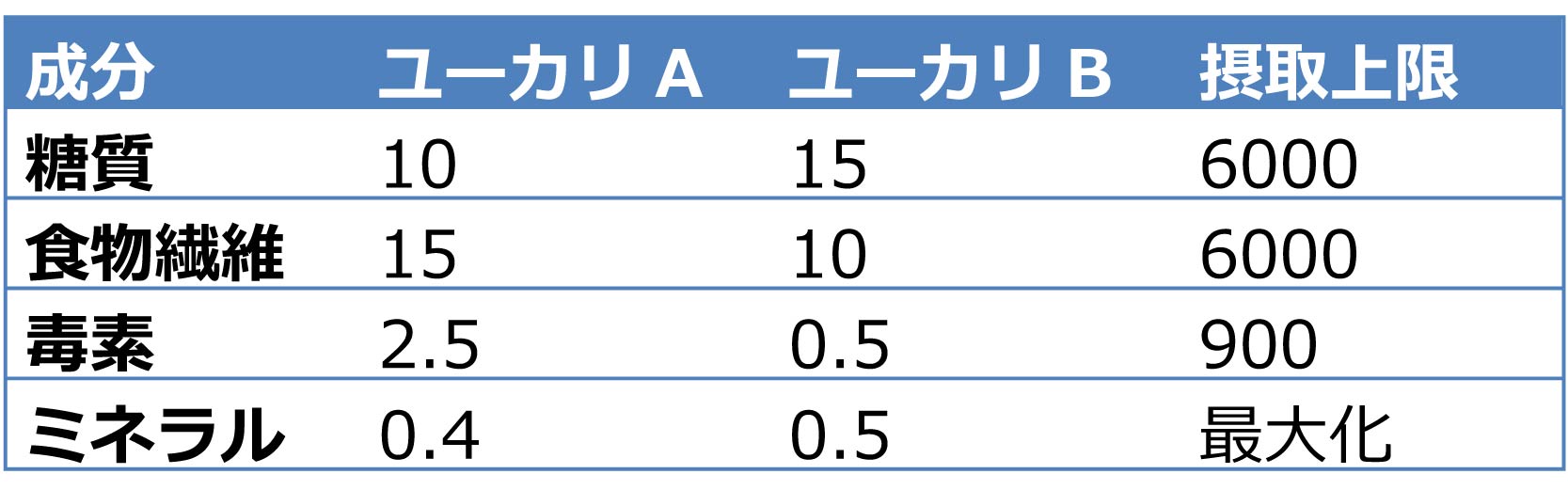
 CCC動物園ではコアラを飼育していますが、近頃ぐうたらし過ぎて太ってしまいました。そこで、ダイエットのために糖質制限をかけて餌を与えることにします。主食のユーカリには糖質の他にも食物繊維、ミネラル、毒素が含まれていますが、ミネラル以外のものは取りすぎるとよくないので、こちらも摂取制限をかけます。
CCC動物園ではコアラを飼育していますが、近頃ぐうたらし過ぎて太ってしまいました。そこで、ダイエットのために糖質制限をかけて餌を与えることにします。主食のユーカリには糖質の他にも食物繊維、ミネラル、毒素が含まれていますが、ミネラル以外のものは取りすぎるとよくないので、こちらも摂取制限をかけます。
成分構成の異なる二つのユーカリをうまく食べ合わせて、なるべく多くのミネラルを摂取するにはどうすればいいでしょうか。
ユーカリ1gあたりの成分表(成分の単位:mg)
今回の目的はミネラル摂取量の最大化でした。
ユーカリAの質量をx、ユーカリBの質量をyとすると、
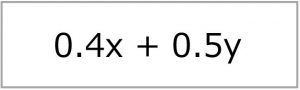
これを最大化することになります。
次に、今回の制約条件を一次不等式で表してみましょう。
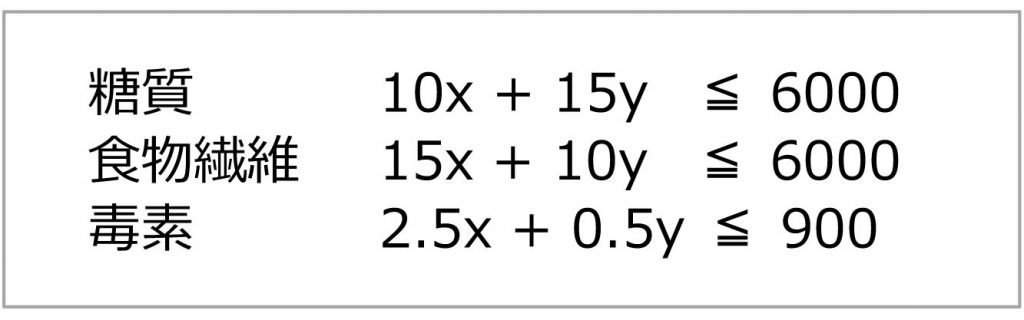
これらの条件式から目的関数を求め、グラフ化すると以下の図のようになります。
横線で塗りつぶされた領域が制約条件を満たす範囲(実行可能領域)となり、この中から最も良い解を探索することになります。

最適化問題の中では最も簡単な問題であり、高速に解を得られる解法が存在します。
その中でも代表的なものとして、以下の2つの方法があります。
| ・単体法 | (Simplex Method) |
| ・内点法 | (Internal Point Method) |
数理最適ソルバでは単体法と内点法を組み合わせて最適解を導出しています。
単体法(Simplex Method)
1947年に米国の応用数学者ジョージ・ダンツィクが発案した手法です。
制約条件をすべて満たす実行可能解から探索を開始し、暫定解が改善する隣接の頂点への移動を繰り返す方法です。
下の図のように実行可能解の領域を表す多面体の外周を回りながら最適解にたどり着くイメージです。
小さな問題には内点法より高速であることが多いと言われています。
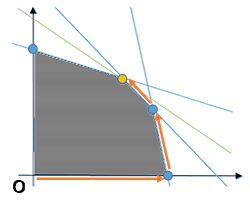
制約条件をすべて満たす実行可能解から探索を開始し、暫定解が改善する隣接の頂点への移動を繰り返す方法です。
下の図のように実行可能解の領域を表す多面体の外周を回りながら最適解にたどり着くイメージです。
小さな問題には内点法より高速であることが多いと言われています。

内点法(Internal Point Method)
1984年にインドの応用数学者ナレンドラ・カーマーカーが発案した手法です。
単体法と同様に実行可能解である初期内点から探索を開始し、暫定解が改善する内点への移動を繰り返す方法です。
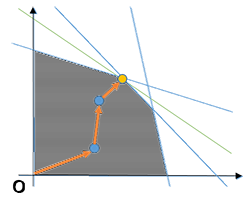
内点の計算が必要なため、解の更新は単体法よりも時間が掛かりますが、大きな問題では、単体法より高速であることが多いと言われています。
単体法と同様に実行可能解である初期内点から探索を開始し、暫定解が改善する内点への移動を繰り返す方法です。

内点の計算が必要なため、解の更新は単体法よりも時間が掛かりますが、大きな問題では、単体法より高速であることが多いと言われています。
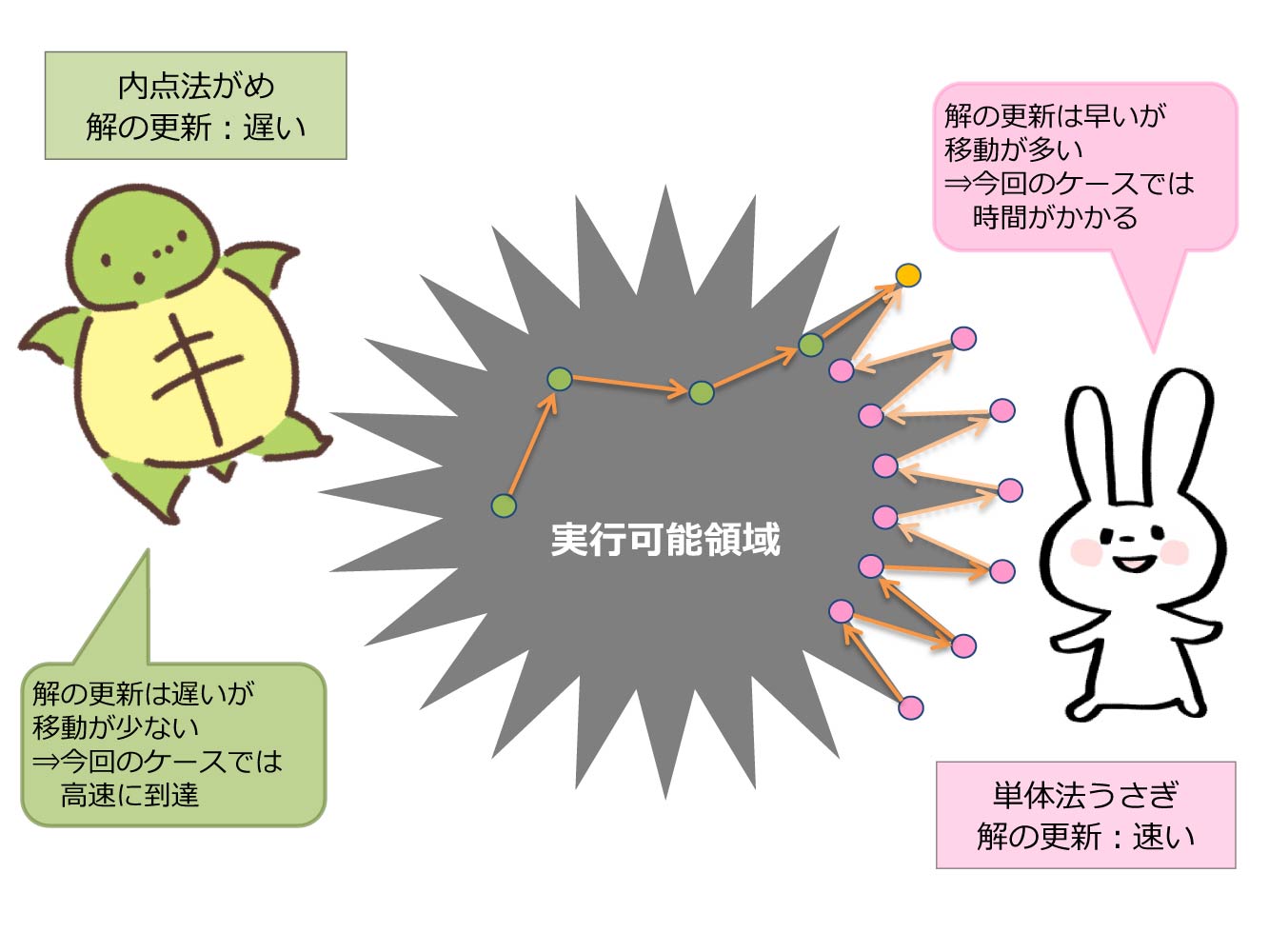
単体法と内点法の比較
例えば下の図のように外周がギザギザとなっている実行可能領域であれば、外側を進む単体法では解の更新が多数発生するため時間がかかってしまうので、内側を進む内点法の方が有利となります。

例題の答え
さて、コアラにはユーカリをそれぞれ何gずつ与えれば良いのでしょうか。
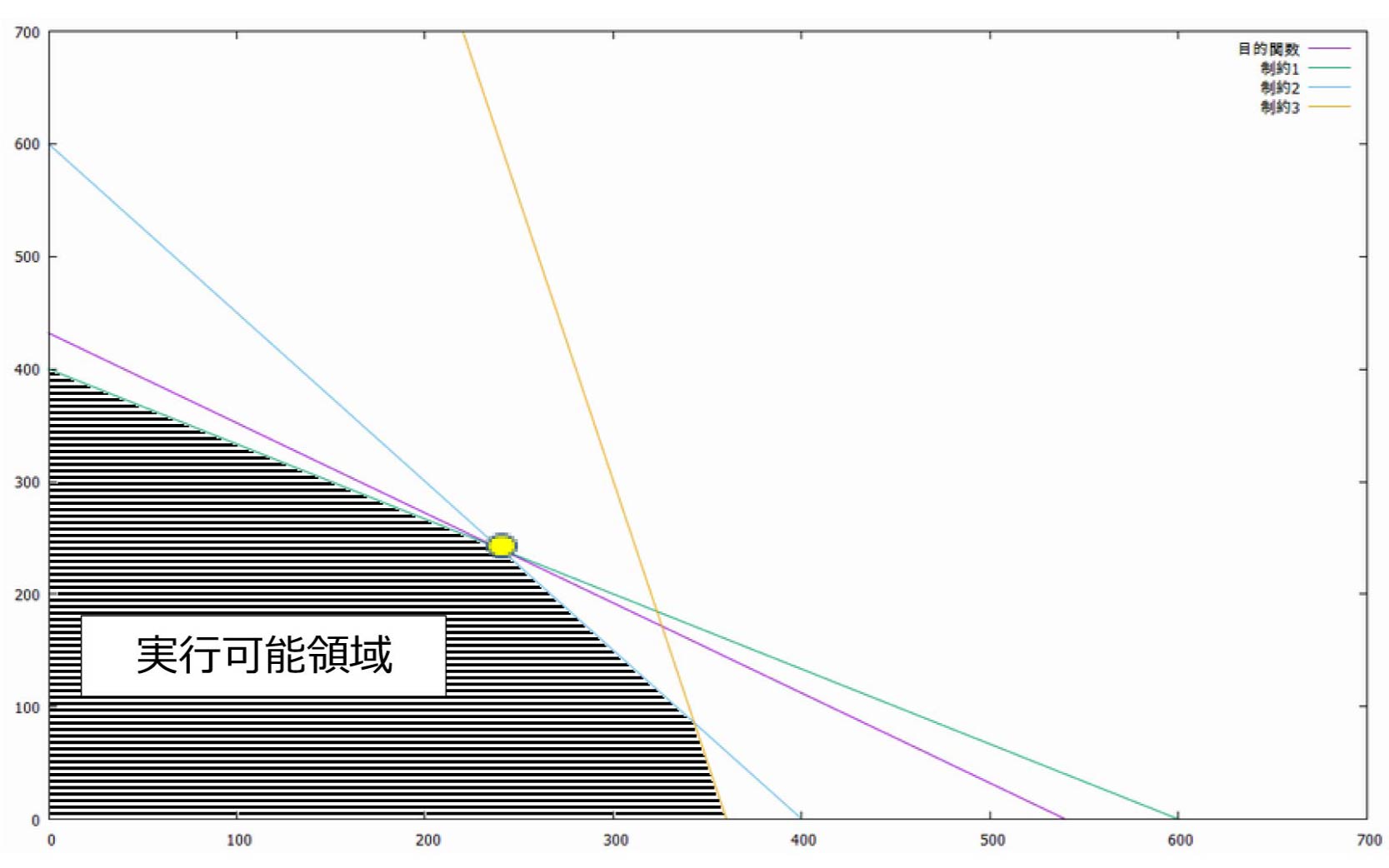
答えは下図の黄色点部分となり、
ユーカリA:240g
ユーカリB:240g
を与えたときにミネラルの摂取が最大値(216mg)となります。
答えは下図の黄色点部分となり、
ユーカリA:240g
ユーカリB:240g
を与えたときにミネラルの摂取が最大値(216mg)となります。

次回は“整数計画問題”と“非線形計画問題”の特徴をご紹介します。
この連載のバックナンバーはこちら




