連載コラム
『数理最適化』
最終回 非線形問題を解く
2017.5.8
最終回となる今回は、第5回にてご紹介した非線形問題を数理最適ソルバを用いて解いてみたいと思います。
⇒第5回の記事はこちら
⇒第5回の記事はこちら
非線形問題の線形緩和
【実行可能領域を示すグラフ】
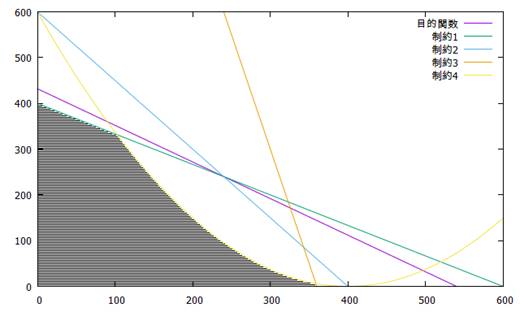

今回の非線形計画問題では、以下のような制約条件がありました。
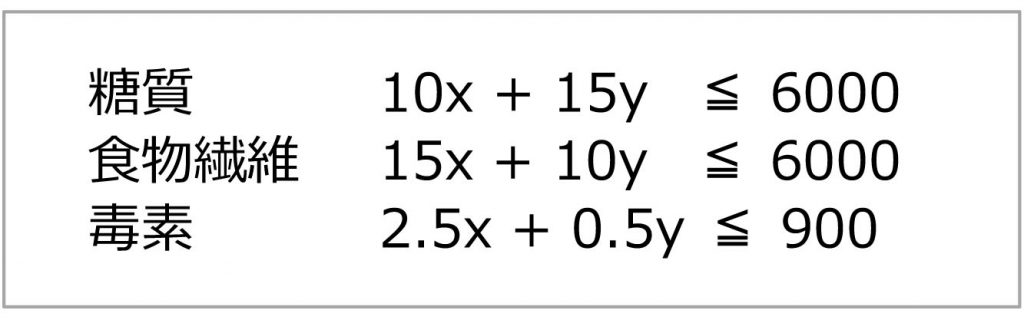
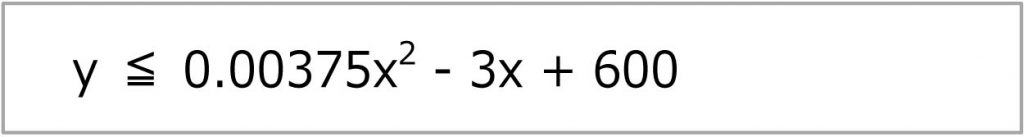
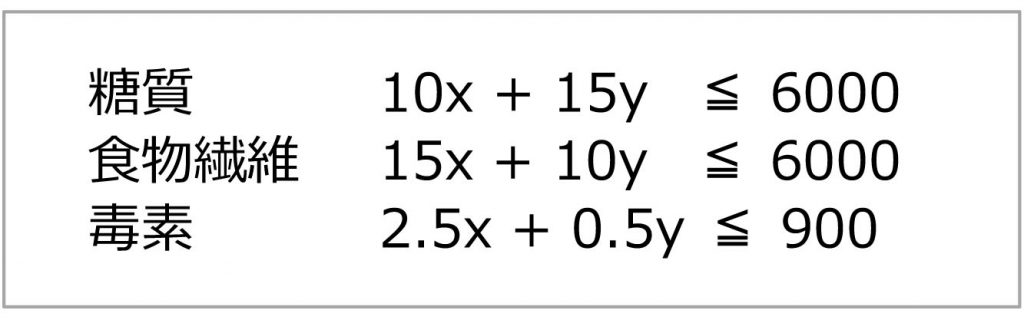
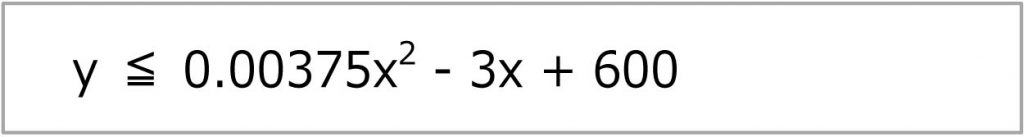
この制約のうち、非線形の制約を線形緩和してみます。
線形緩和とは、曲線を“直線のあつまり”として疑似的に捉えることです。
以下のように区間に区切って直線化していくことで、元の曲線と同じような“直線の集まり”となります。
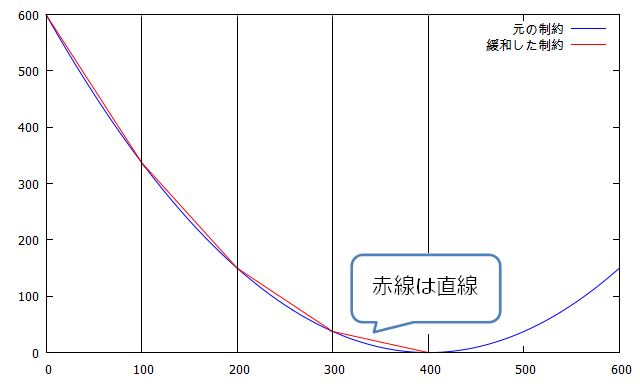
線形緩和とは、曲線を“直線のあつまり”として疑似的に捉えることです。
以下のように区間に区切って直線化していくことで、元の曲線と同じような“直線の集まり”となります。

このように線形緩和した上で、数理最適ソルバを用いて解を求めてみると、以下のようになりました。


ユーカリX:103.4g
ユーカリY:331.0g
上記のときに、
・摂取可能なミネラル:206.9mg
・ユーカリの費用: 60,110円
・誤差0.02%
ユーカリY:331.0g
上記のときに、
・摂取可能なミネラル:206.9mg
・ユーカリの費用: 60,110円
・誤差0.02%
ここで元の制約条件を振り返ってみましょう。
ユーカリを購入するための費用は60,000円と決まっていました。今回の解では費用が60,110円となっており、60,000円以上に上振れしてしまうことを示しています。

毒素や食物繊維の摂取量であれば少しぐらいの上振れは許容できますが、費用が予算よりも超過してしまうと動物園の経営に影響が出るかもしれません。
費用が上振れしないように線形緩和方法を見直してみましょう。
曲線上であれば費用はぴったり60,000円となりますが、凸の内側では60,000円以上となり、凸の外側では60,000円以下となることが分かります。
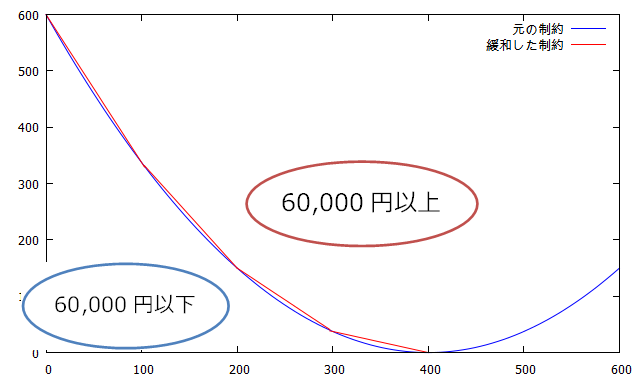
曲線上であれば費用はぴったり60,000円となりますが、凸の内側では60,000円以上となり、凸の外側では60,000円以下となることが分かります。

線形緩和した直線は凸の内側に入っているので、凸の外側にするために直線全体をマイナス方向に並行移動します。
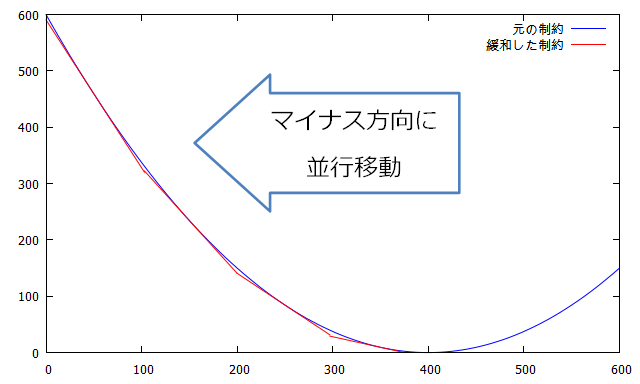
上図の通り、線形緩和した直線を凸の外側へ移動することができました。

上図の通り、線形緩和した直線を凸の外側へ移動することができました。
【実行可能領域を示すグラフ:線形緩和見直し後】
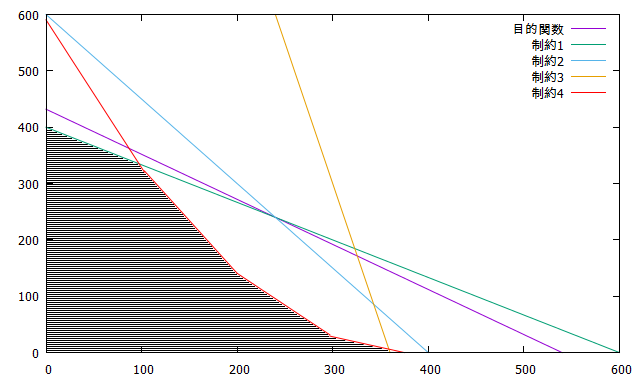

修正した形で、改めて数理最適ソルバを用いて解を求めてみると、結果は以下の通りです。
ユーカリX:97.3g
ユーカリY:335.1g
上記のときに、
・摂取可能なミネラル:206.5mg
・ユーカリの費用: 59,149円
・誤差:-0.19%
ユーカリY:335.1g
上記のときに、
・摂取可能なミネラル:206.5mg
・ユーカリの費用: 59,149円
・誤差:-0.19%

予算を厳守しながら、コアラにとって最適なユーカリX、Yの食べ合わせバランスを得ることができました。
実務の場面では、単に線形緩和するだけでは満足な結果は得られず、このように制約条件の背景も踏まえて試行錯誤する場面もあるかと思います。
数理最適ソルバを利用する技術だけではなく、適用する事象への理解が重要であることが分かりました。
数理最適ソルバを利用する技術だけではなく、適用する事象への理解が重要であることが分かりました。
さいごに
全6回にわたり、数理最適化に関してご紹介いたしました。
とっつきにくい分野かもしれませんが、このコラムにて興味を持って頂ければ幸いです。
とっつきにくい分野かもしれませんが、このコラムにて興味を持って頂ければ幸いです。
弊社は
・世界最速の数理最適ソルバを利用した製品(ecoLLabo WFM)
・様々な業務のシステム化をお手伝いしてきた経験
の両方を兼ね備えておりますので、必ずや、業務最適化を必要とするお客さまのお役に立てると考えております。
・世界最速の数理最適ソルバを利用した製品(ecoLLabo WFM)
・様々な業務のシステム化をお手伝いしてきた経験
の両方を兼ね備えておりますので、必ずや、業務最適化を必要とするお客さまのお役に立てると考えております。
良きパートナーとして、弊社をご指名頂ければ幸いです。
この連載のバックナンバーはこちら




